極限存在和連續的關系
在數學分析中,極限存在和函數連續是兩個密切相關的概念,但它們并不完全相同。以下是這兩個概念的簡要說明以及它們之間的關系:
1. 極限存在:
- 極限存在是指對于一個函數在某一點的極限,如果當自變量趨近于這一點時,函數值趨近于某個確定的值,那么我們說這個極限存在。
- 形式上,對于函數\( f(x) \)在點\( c \)的極限,如果存在一個實數\( L \),使得對于任意給定的正數\( \epsilon \),都存在一個正數\( \delta \),使得當\( 0 < |x - c| < \delta \)時,有\( |f(x) - L| < \epsilon \),那么我們就稱\( \lim_{x \to c} f(x) = L \)。
2. 函數連續:
- 函數連續是指函數在某一點的極限值與函數在該點的值相等。也就是說,如果\( \lim_{x \to c} f(x) = f(c) \),那么稱函數\( f \)在點\( c \)連續。
- 連續性還可以推廣到區間上,如果函數在區間\( I \)上每一點都連續,那么稱函數在區間\( I \)上連續。
極限存在與連續的關系:
- 如果函數在某點的極限存在,但不一定意味著該函數在該點連續。極限存在是連續性的必要條件,但不是充分條件。也就是說,如果函數在某點連續,那么該點的極限一定存在,并且等于函數在該點的值。
- 但是,如果函數在某點的極限存在,但不等于函數在該點的值(如果該點在函數的定義域內),那么函數在該點不連續。
例子:
- 考慮函數\( f(x) = \frac{1}{x} \),它在\( x = 0 \)處的極限是不存在的,因為當\( x \)趨近于0時,函數值會無限增大或減小,所以它在\( x = 0 \)處不連續。
- 另一方面,考慮函數\( f(x) = |x| \),它在\( x = 0 \)處的極限是存在的,且等于0,同時函數在\( x = 0 \)處的值也是0,所以函數在\( x = 0 \)處是連續的。
總結來說,極限存在是連續性的必要條件,但不是充分條件。函數在某點連續意味著該點的極限存在且等于函數在該點的值。
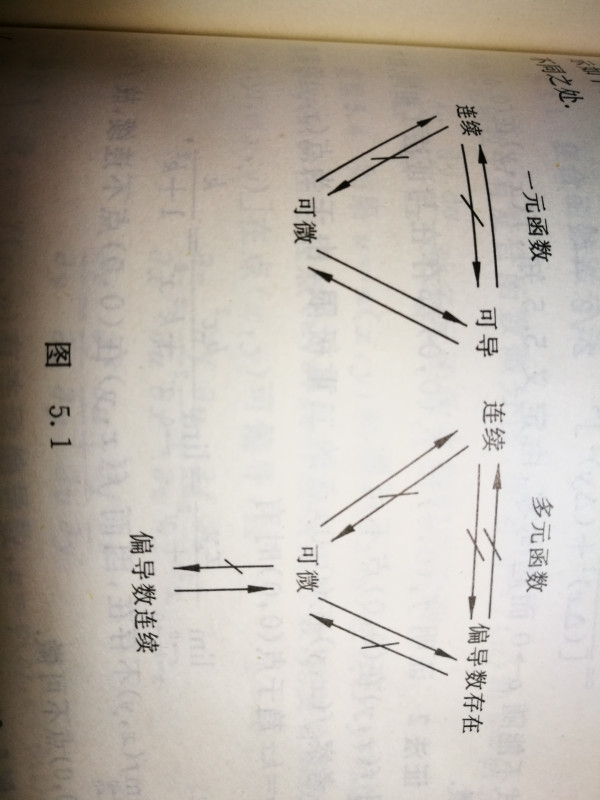
連續極限可導三者什么關系
在數學分析中,連續、極限和可導是描述函數性質的三個重要概念。它們之間的關系如下:
1. 連續性:如果函數在某點的極限值等于該點的函數值,則稱該函數在該點連續。對于函數在某區間連續,意味著在該區間內的每一點都是連續的。
2. 極限:極限是描述函數在某點附近的行為,特別是當自變量趨近于某一點時,函數值趨近于某個特定的值。極限是微積分中的基礎概念,連續性和可導性都與極限有關。
3. 可導性:如果函數在某點的導數存在,即該點的瞬時變化率存在,那么稱該函數在該點可導。導數可以看作是函數在某點的切線斜率。
它們之間的關系可以總結如下:
- 連續性不一定意味著可導:一個函數在某點連續,并不意味著它在該點可導。例如,函數 \( f(x) = |x| \) 在 \( x = 0 \) 處是連續的,但不可導。
- 可導性蘊含連續性:如果一個函數在某點可導,那么它在該點也必定連續。因為可導意味著極限存在,而連續性的定義也要求極限存在且等于函數值。
- 極限的存在性是連續性和可導性的基礎:無論是連續還是可導,都涉及到極限的存在性。連續性要求函數在某點的極限值等于該點的函數值,而可導性要求導數(即極限)存在。
簡而言之,可導性是連續性的一種更強的條件,而連續性與極限的存在性緊密相關。
有極限未必連續的例子
在數學分析中,極限和連續是兩個相關但獨立的概念。一個函數在某點的極限存在,并不意味著該函數在該點連續。連續性意味著函數在某點的極限值等于函數在該點的值。以下是一些函數在某點極限存在但不一定連續的例子:
1. 函數定義不完整:
\[ f(x) = \begin{cases}
1 & \text{if } x \neq 0 \\
0 & \text{if } x = 0
\end{cases} \]
這個函數在 \( x = 0 \) 處的極限是 0,因為當 \( x \) 接近 0 時,\( f(x) \) 接近 0。但是,函數在 \( x = 0 \) 處不連續,因為 \( f(0) \neq \lim_{x \to 0} f(x) \)。
2. 振蕩函數:
\[ f(x) = \sin(\frac{1}{x}) \]
當 \( x \) 接近 0 時,這個函數在 -1 和 1 之間振蕩,因此 \( \lim_{x \to 0} f(x) \) 不存在。但是,如果我們考慮 \( f(x) \) 在 \( x \neq 0 \) 時的極限,它在每個非零點都有定義,并且可能存在極限。
3. 函數在某點不定義:
\[ f(x) = \frac{1}{x} \]
這個函數在 \( x = 0 \) 處沒有定義,但它在 \( x \neq 0 \) 時是連續的。盡管 \( \lim_{x \to 0} f(x) \) 存在(趨向于正無窮或負無窮),但函數在 \( x = 0 \) 處不連續。
4. 函數在某點有跳躍不連續:
\[ f(x) = \begin{cases}
x & \text{if } x \leq 0 \\
x + 1 & \text{if } x > 0
\end{cases} \]
這個函數在 \( x = 0 \) 處有一個跳躍,因此不連續。但是,我們可以計算出 \( \lim_{x \to 0^-} f(x) = 0 \) 和 \( \lim_{x \to 0^+} f(x) = 1 \),所以極限存在但不相等。
這些例子展示了函數在某點極限存在和函數在該點連續是兩個不同的概念。連續性要求極限值等于函數在該點的值。

 微信掃一掃打賞
微信掃一掃打賞